Deutsche Einführung

Grundsätzliches

Euler ist ein numerisches Laboratorium. Numerisch deswegen, weil Euler keine symbolischen Termumformungen vornimmt, wie z.B. Maple. Die Stärken des Programms liegen daher in der viel höheren Geschwindigkeit und in der einfachen Handhabung von großen Datenmengen.

Am stärksten verwandt ist Euler mit MatLab und seinen Nachahmern, wie SciLab. Als 1988 die erste Version von Euler entstand, steckte allerdings auch MatLab noch in den Kinderschuhen. Daher hat Euler zwar den gleichen Ansatz wie MatLab, ist aber nicht voll kompatibel. Ich habe in vielen Fällen die Syntax genommen, die ich für besser und einfacher hielt.

Im Prinzip ist Euler eine Matrixsprache. Es existieren sehr mächtige Funktionen, um Matrizen und Vektoren zu verwalten und modifizieren. Natürlich kann man das für lineare Algebra und Geometrie benutzen. Der Haupteinsatz liegt jedoch in der Erstellung von Daten- und Funktionstabellen.

Bevor wir aber dazu kommen, wollen wir kurz die Befehlszeile von Euler vorstellen. In der Befehlszeile können Sie Kommandos eingeben, die Euler berechnen oder ausführen soll. Die Zeile dient außerdem zur Eingabe von Funktionen, sofern diese nicht aus externen Dateien gelesen werden. Geben Sie zunächst ein

>(5*4+3/2)/4^2
      1.34375 

Geben Sie diesen Befehl in der Kommandozeile ein und drücken Sie anschließend die Eingabetaste. Falls Sie einen Fehler gemacht haben, so können Sie mit Cursor-Hoch in diese Zeile zurückwechseln und den Fehler korrigieren. Euler berechnet das Ergebnis sofort. Deswegen nennt man solche Systeme interaktiv. Natürlich werden die üblichen Rechenregeln (die Operatorpriorität) beachtet. Beispielsweise wird 4^2 (steht für 4 hoch 2) vor der Division berechnet. Euler kennt auch die üblichen mathematischen Funktionen. Außerdem kennt es komplexe Zahlen.

>longformat; sin(1+1i)
                1.298457581416+0.6349639147847i 

Hier wurde außerdem noch auf ein längeres Ausgabeformat umgeschaltet. Das Semikolon hinter dem longformat-Befehl verhindert die Ausgabe des Befehlsergebnisses. Man schaltet übrigens mit shortformat zurück.

>longestformat; 1/3
            0.33333333333333331 

Dieses Format ist so lang, dass die interne Rundung deutlich wird. Auf Wunsch gibt Euler auch Brüche aus.

>fracformat; 1+1/2+1/3+1/4+1/5
             137/60 

Intern wird jedoch immer mit double-Zahlen gerechnet.

Wie man Vektoren eingibt, wird weiter unten im Abschnitt über lineare Algebra besprochen. Wir erzeugen hier als Beispiel für die Verwendung von Euler anstelle eine Programmiersprache eine Reihe von Zufallszahlen.

>z=random(1,1000);

Falls Sie das Semikolon vergessen haben, werden die 1000 Zahlen ausgegeben. Dies können Sie mit der Escape-Taste abbrechen.

Mit dem obigen Befehl wird eine 1x1000-Matrix (also einen Zeilenvektor) mit gleichverteilten Zufallszahlen zwischen 0 und 1 erzeugt. Dieser Vektor wird als Variable z festgehalten. Es ist nun einfach, mit diesen Zahlen zu hantieren. Z.B. berechnet man den Mittelwert mit

>shortformat; m=sum(z)/length(z)
     0.509271

Statt length(z) kann natürlich auch einfach 1000 eingesetzt werden, oder cols(z), was die Anzahl der Spalten von z ergibt. sum(z) berechnet die Zeilensumme von Matrizen, in diesem Fall also einfach die Summe der 1000 Zahlen.

Damit ist es nun nicht schwer, die Stichprobenstreuung zu berechnen.

>sqrt(sum((z-m)^2)/(length(z)-1))
     0.285003

Euler enthält auch eine Programmiersprache, mit der sich neue Funktionen schreiben lassen. Diese Funktionen befinden sich in externen Dateien, die geladen werden müssen. Daher läßt sich derselbe Effekt wie oben auch mit den folgenden Befehlen erreichen.

>load statist
Statistical Functions
>mean(z)
     0.509271 
>dev(z)
     0.285003 

Um etwas Komplizierteres vorzuführen, zählen wir, wie oft eine Zufallszahl größer ist als die beiden benachbarten. Die beiden Randelemente sollen nicht mitgezählt werden. Das geht so

>sum(z[2:999]>z[1:998] && z[2:999]>z[3:1000])
          323 

Wie funktioniert das? Der Vektor 2:999 ist einfach der Vektor der Zahlen 2,3,4,...,999. Setzt man diesen Vektor als Index für z ein, so werden alle Elemente mit diesen Indizes aus z ausgewählt und in einen neuen Vektor eingetragen. Anschließen werden zwei solche Vektoren miteinander verglichen. Dies ergibt 1 an allen Stellen, an denen der Vergleich zutrifft und 0 sonst. Dann werden noch die beiden Vergleichsresultate gliedweise mit und verknüpft. Die Summe der vorhanden Einser zählt genau das, was wir wollen.

Dieses Beispiel demonstriert recht gut, was man mit Euler anfangen kann. Es ersetzt in vielen Fällen eine Programmiersprache. Dabei stehen zudem noch mächtige Funktionen in einfacher Weise zur Verfügung, für die man sonst eine Bibliothek bräuchte. Euler ist quasi ein interaktives Laboratorium der Numerik.

Einfache Plots

Da Funktionen auf Vektoren gleidweise wirken, könnte man einen einfachen 2D-Plot folgendermaßen erzeugen

>t=-5:0.01:5; xplot(t,sin(2*t)*t);

Dies erzeugt einen Plot der Funktion sin(2*t)*t zwischen -5 und 5, weil t ein Vektor ist, der die Werte -5,...,5 enthält mit einer Schrittweite von 0.01. Das Ganze sieht dann so aus

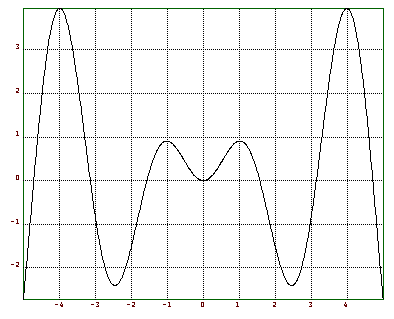
Als Parameter für xplot werden zwei Vektoren erwartet mit x- und y-Koordinaten der Punkte. Die Punkte werden durch Linien verbunden. Daher kann man auch andere Kurven in der Ebene plotten, z.B. erhält man den Einheitskreis durch

>t=linspace(0,2*pi,1000); xplot(cos(t),sin(t));

Allerdings muss man das Ausgabefenster in die richtigen Proportionen bringen, sonst ist der Kreis eine Ellipse. Die Ausgabe wird dabei angepasst. Der Vektor t wird hier nicht mit Hilfe der Schrittweite wie oben erzeugt, sondern mit der Funktion linspace, die die beiden Grenzen und die Anzahl der Teilintervalle erwartet.

Hier ein Beispiel für eine hübsche Figur.

>clg; hold; plot(sin(4*t),cos(5*t)); hold;

Der Trick mit dem hold sorgt dafür, dass kein Rahmen gezeichnet wird. Im Prinzip dient dies dazu, Plots mit anderen zu übermalen. Das Kommando clg löscht die alte Grafik.

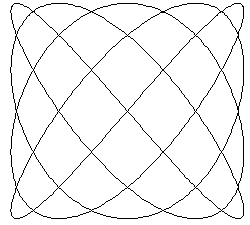
Einfacher als dies alles ist die Verwendung von Funktionen in Strings. Die obige Funktion läßt sich wesentlich einfacher mittels

>fplot("sin(2*x)*x",-5,5);

plotten. Der String kann dabei entweder eine Funktion in der Variablen x enthalten oder den Namen einer selbstprogrammierten Funktion.

Solche selbstdefinierten Funktionen lassen sich entweder direkt in der Kommandozeile eingeben, oder von externen Dateien laden. Wir geben eine Funktion ein, die durch eine Fallunterscheidung definiert ist. Sie soll x^2 rechts von 0 und -x^3 links von 0 sein.

>function f(x)
$if x>0; return x^2;
$else return -x^3;
$endif;
$endfunction

Dies definiert die verlangte Funktion. Die Eingabe erfolgt interaktiv, wobei durch die Änderung des Cursors signalisiert wird, dass Euler sich im Eingabemodus befindet. Die verwendete Programmiersprache sollte ziemlich einleuchtend sein. Man beachte, dass x keinen Datentyp hat. Die Funktion funktioniert daher für alle Datentypen, die Euler verwenden kann und die in der Funktion Sinn machen, insbesondere für reelle und komplexe Zahlen. Für Intervalle, die 0 enthalten arbeitet die Funktion übrigens ebenfalls nicht korrekt.

Für Vektoren von Zahlen arbeitet die Funktion ebenfalls nicht richtig. Daher gibt es die möglichkeit eine gegebene Funktion auf alle Elemente eines Vektors anzuwenden.

>function fvec(x)
$return map("f",x);
$endfunction

Nun kann die Funktion auch geplottet werden.

>fplot("fvec",-1,1);

Mit einem Trick geht das ganze auch in einer Zeile.

>fplot("(x>=0)*x^2+(x<0)*(-x^3)",-1,1);

Natürlich kann man auch einzelne Punkte zeichnen, oder Balken. Als Beispiel erzeugen wir ein Bild der Binomialverteilung und legen die entsprechende Normalverteilung darüber.

>n=20; b=bin(n,0:n)/2^n;
>setplot(-0.5,n+0.5,0,0.2); xplotbar((0:n)-0.5,0,1,b);
>color(10); style("m[]"); hold on; mark(0:n,b); hold off;
>color(4); linewidth(2); t=linspace(0,n,300); m=10; s=sqrt(20/4);
>hold on; plot(t,1/(sqrt(2*pi)*s)*exp(-(t-m)^2/(2*s^2))); hold off;

Hier werden verschiedene Stile und Farben gesetzt. Diese können alle mit reset() zurückgesetzt werden. Barplots sehen etwas kompliziert aus, weil sie die x-y-Koordinaten der Balken, sowie deren Weiten und Höhen als Parameter erwarten. Einfacher ist ein mark-Plot, den wir als zweites über die Zeichnung legen. Beachten Sie, dass alle Plots gemäß den in setplot eingestellten Grenzen skaliert werden.

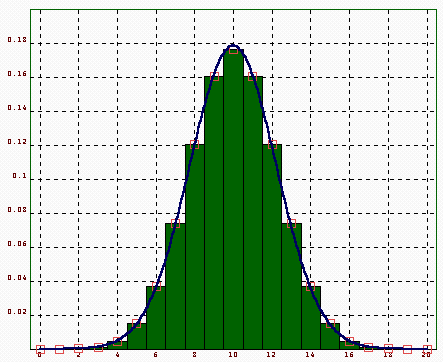
Kurvendiskussion

Kurvendiskussionen kann man mit Funktionstabellen durchführen, genau wie die Grundfunktionen des Plottens. Es existieren aber genau wie dort Funktionen, die direkt mit Ausdrücken oder benutzerprogrammierten Funktionen arbeiten. Als Beispiel betrachten wir die Funktion sin(t)/t.

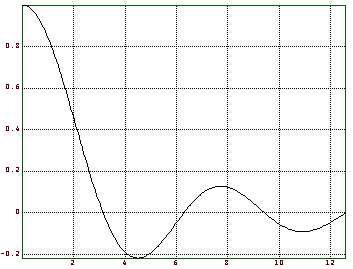
Zuerst verschaffen wir uns einen Überblick durch Plotten.

>f="sin(x)/x";
>fplot(f,epsilon,4*pi);

Dieses Mal haben wir darauf verzichtet, eine Fallunterscheidung zu machen, und speichern die Funktion einfach als Ausdruck in einem String. Deswegen werden wir im Punkt 0 immer eine Fehlermeldung erhalten. Um das zu vermeiden, plotten wir von einem kleinen positiven Wert epsilon aus. Dieser Wert wird auch dazu verwendet, Zahlen auf ungefähre Gleichheit zu testen (a~=b).

Nun berechnen wir die erste Nullstelle, die natürlich Pi ist.

>longformat; secant(f,3,4)
3.14159265359

Von Interesse ist vielleicht auch das Integral, die wir sowohl mit Gauß als auch mit Romberg berechnen, und die Ableitung.

>romberg(f,epsilon,pi)
          1.85193705198 
>gauss(f,epsilon,pi)
          1.85193705198 
>dif(f,pi)
       -0.3183098551892

Wo ist nun das Minimum zwischen 2 und 6?

>m=fmin(f,2,6)
         4.493409448108 
>dif(f,m)
    -2.457683194734e-08 

Wir wollen zum Abschluß das Integral von f von 0 bis t als Funktion definieren. Dazu verwenden wir eine Funktiondefinition. Die Gaußintegration funktioniert schon korrekt mit Vektoren, so dass auch unsere Funktion mit Vektoren arbeiten wird.

>function g(t)
$return gauss("sin(x)/x",0,t);
$endfunction
>fplot("g",epsilon,3*pi);

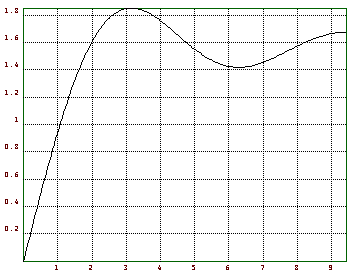
Plots von Funktionen mit zwei Variablen

Neben den im vorigen Kapitel erwähnten Plots, die praktisch eindimensional sind, kann man auch Funktionen von zwei Variablen zeichnen. Die einfachste Art und Weise ist ein mesh-Plot, der die Funktion in drei Dimensionen zeigt.

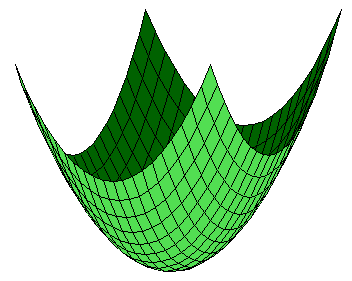
Dieser Plot wird mit

>x=-1:0.1:1; y=x'; mesh(x^2+y^2);

erzeugt. Dabei laufen beide Variablen von -1 bis 1. x ist dabei ein Zeilenvektor und y ein Spaltenvektor. Werden solche Vektoren verknüpft (hier durch +), so entsteht eine Matrix aus Werten die alle möglichen Kombinationen enthält, hier also die Elemente x[i]^2+y[j]^2 für alle i und j. Diese Matrix wird bei der obigen Zeichnung als Niveauhöhe benutzt.

Wie im vorigen Paragraphen kann man auch mit

>f3dplot("x^2+y^2",-1,1,-1,1);

die Funktion gezeichnet werden.

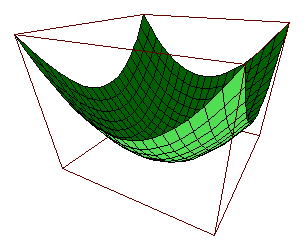
Interessant sind auch Höhenlinien einer Funktion, die sich mit

>fcontour("x^2+x*y^3",50);

erzeugen lassen.

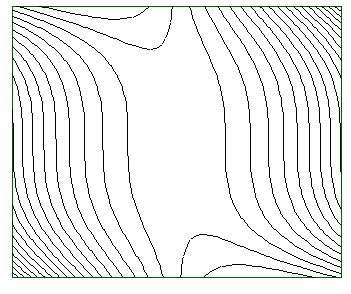
Dabei wird 50 als zusätzlicher Parameter übergeben, der für die Feinheit des Plots sorgt. Es sind weitere zusätzliche Parameter (der x- und y-Bereich, und die Anzahl der Höhenlinien) möglich, über die man mit

>help fcontour

Auskunft erhält. Einen guten Überblick über eine Funktion verschaffte ein kombinierter Dichte und Höhenlinien-Plot mit

>color(5); fcd("x^2+x*y^3);

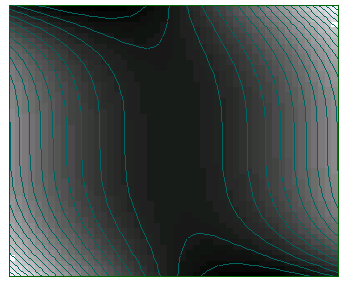
Die Abbildung leidet etwas unter der Reduktion auf 256 Farben.

3 Variablen

Euler kann auf sowohl einfache Weise, als auch auf flexiblere Weise Plots von dreidimensionalen Oberflächen erzeugen. Über die Variationsbreite der möglichen Plots gibt die Demo Auskunft, die man mit

>load demo

(oder dem Menü) startet. Wir zeigen hier deswegen nur ein Beispiel.

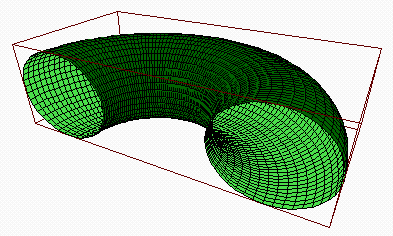
Um dieses Bild zu erzeugen, muss man offenbar eine Karte der Oberfläche anfertigen. Dies geschieht mit Hilfe der folgenden Befehle

>x=linspace(0,pi,80); y=linspace(-pi,pi,40)';
>X=cos(x)*(1+0.5*cos(y)); Y=sin(x)*(1+0.5*cos(y)); Z=0.5*sin(y);
>framedsolid(X,Y,Z,3);

Der zusätzliche Parameter 3 ist ein Streckungsfaktor, der dafür sorgt, dass alles schön im Bild ist. Der Blickwinkel kann mit Hilfe von view eingestellt werden.

>view(7,1.5,-1,-0.5); framedsolid(X,Y,Z,3);

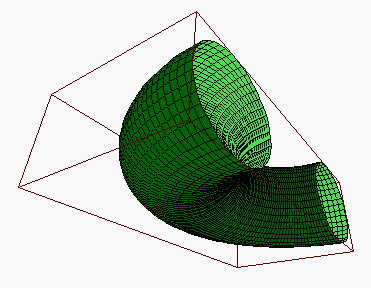
Lineare Algebra

Es existieren die üblichen Funktionen der linearen Algebra, einschließlich mehrere Funktionen zur Berechnung von Eigenwerten, und zur Lösung von Optimierungsproblemen. Damit es nicht zu leicht wird, verwenden wir gleich eine schlecht konditionierte Matrix.

>a=0.34567; d=0.87654; c=round(sqrt(a*d),5);
>A=[a,c;c,d]
      0.34567       0.55045 
      0.55045       0.87654 

Diese Matrix wurde so erzeugt, dass die Determinante sehr klein ist. Die Eingabe einer Matrix erfolgt zeilenweise, wobei die Spalten durch Kommas und die Zeilen durch Semikolon getrennt werden.

>det(A)
  -1.6207e-06 

In der Tat ist die Determinante klein. Wie lösen nun ein künstliches Gleichungssystem, dessen Lösung der Vektor (1,1) sein muss.

>b=A.[1;1]
      0.89612 
      1.42699 
>A\b
            1 
            1

Der Punkt steht für die Matrizenmultiplikation und der Schrägstrich A\b für die Lösung von Ax=b. Es treten hier keinerlei numerische Probleme auf. Verändert man aber A ein klein wenig, so ensteht eine komplett andere Lösung.

>[a,c;c,d+0.00001]\b
      3.99809 
    -0.882734 

Dies spricht für eine schlechte Kondition der Matrix. Wir berechnen die Eigenwerte und den Quotient aus dem Betrag des größten und des kleinsten Eigenwertes.

>l=eigenvalues(A), max(abs(l))/min(abs(l))
            -1.32604e-06+0i                  1.22221+0i 
       921701 

Man kann auch alle Eigenwerte und Eigenvektoren auf einmal berechnen. Die Eigenvektoren werden dabei normiert, so dass wir sofort eine Diagonaldarstellung bekommen.

>{l,v}=eigen(A); v
               -0.846862+0i                 0.531812+0i 
                0.531812+0i                 0.846862+0i 
>D=diag([2,2],0,l)
            -1.32604e-06+0i                        0+0i 
                       0+0i                  1.22221+0i 
>v'.D.v
                 0.34567+0i                  0.55045+0i 
                 0.55045+0i                  0.87654+0i

Wir wollen nun annehmen, dass A auf 5 Stellen genau sei, wie das aufgrund der Zahlenwerte zu vermuten ist. In Euler können wir dazu die Intervallrechnung verwenden.

>B=A+~-0.000005,0.000005~
Column 1 to 1:
                      ~0.345665,0.345675~ 
                      ~0.550445,0.550455~ 
Column 2 to 2:
                      ~0.550445,0.550455~ 
                      ~0.876535,0.876545~ 
>B\b
Determinant may be 0

Wie man sieht, läßt sich das Gleichungssystem nicht mehr lösen. Nimmt man eine Genauigkeit von 6 Stellen an, so wird ein Lösungsintervall berechnet. Die Funktion ilgs tut dies in etwas optimalerer Form, so dass die Intervalleinschließung kleiner wird. Am genauesten Wäre der Schnitt zwischen beiden Lösungsintervallen.

>(A+~-0.0000005,0.0000005~)\b
                         ~-7.057,2.32962~ 
                               ~0.17,6.1~ 
>ilgs((A+~-0.0000005,0.0000005~),b)
                       ~-2.10793,4.10793~ 
                      ~-0.951715,2.95171~ 

Weitere Beispiele dieser Art finden sich in der Demo.

Weitere Hilfe

In dieser Einführung konnten wir lediglich einen kleinen Einblick in Euler geben. Als weitere Experimente sollte man die mitgelieferten Notebooks laden und ausführen. Interessant ist hier die deutsche Einführung in Form eines Notebooks. Unter Windows werden Notebooks mit der Kommandozeile geladen. In Unix verwendet man das notebook Kommando.

Eine Demo wird mittels

>load demo

gestartet, oder in Windows über das Menü. Alternativ gibt es eine selbstablaufende Demo.

>load autodemo

Beide werden, wie alle Euler-Kommandos mit der Excape-Taste abgebrochen. Sie können ruhig auch andere Euler-Files laden, die mitgeliefert wurden, ebenso wie die anderen Notebooks.

Die Dokumentation von Euler befindet sich in HTML-Form im Unterverzeichnis doc. Bei der Installation der Windows-Version erhalten Sie Links darauf im Startmenü. Falls Sie unter Linux mit RPM installiert haben, so finden Sie die Hilfe an der üblichen Stelle.

Außerdem steht eine Online-Hilfe zur Verfügung, die sie mit dem Kommando

>help fplot

aufrufen können. Es wird entweder ein eingebauter Befehl erklärt, oder die Hilfezeilen einer Programmdefinition ausgedruckt.

Die Hilfe im Help-Menü von Windows erklärt lediglich die Besonderheiten der Windows-Oberfläche.

Abschließend bleibt mir noch, Ihnen viel Erfolg mit Euler zu wünschen.